The driver, the navigator and the manager
The new AI is making good progress; I’d say it’s about 90% finished. (The other 90% remains to be done.) After writing the code, it cleanly fell apart into three largely independent modules. I like to name my classes after corresponding real-world things, so these are called the Driver, the Navigator and the Manager.
- The Driver is the one at the wheel. He has no knowledge about the structure of the world, or about obstacles. All he knows is a single point, the target. He assumes that there is a clear path between him and the target, and will attempt to drive towards it.
- The Navigator is the one who reads the map. He knows the structure of the map and the obstacles, and plots a course to a certain objective. He then hands over target points to the Driver one by one.
- The Manager is the upper level. He makes the strategic decisions, weighing the benefits of each potential objective against the costs, then instructs the Navigator to set a course towards the best objective.
This blog post is about the Driver. The Navigator and the Manager will follow in one or two subsequent posts.
Due to the control scheme, the Driver’s job is not easy. Ironically, this occurs because of the very same problems that a human Driver has. First, you have to turn the cart to face in the direction you want to go; then, you fire the thrusters to propel you in that direction. Throughout all this, you have to take your current linear momentum (velocity) and angular momentum (spin) into account.
The Driver wants to give the cart a velocity in the direction of the target. The first stage, therefore, is to compute the difference between the current velocity and the desired velocity:
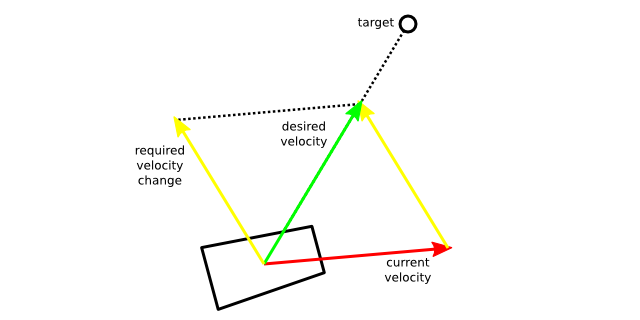
However, to fire the thrusters in the direction of the velocity change, we first need to turn the cart to face that way (or away from it, if we decide to use the reverse thrusters). The first version makes the cart turn if it’s far from the right direction; fires just one thruster if it’s close to the mark, but not quite there yet; and fires both thrusters if it’s head-on. But all this leads to a problem of ‘overshoot’: we turn in the direction of the yellow arrow, but after that, we just keep on spinning and quickly go out of alignment again!
It gave me some headaches to compensate for this overshoot. The trick was to think in terms of angle, angular velocity, and angular acceleration. At any given point in time, the cart has a certain angle (from 0 to 360 degrees, or from 12 to 12 hours if you like) and a certain angular velocity (degrees per second). For example, the seconds hand on a clock goes a full 360 degrees in 60 seconds, so its angular velocity is 360 / 60 = 6 degrees per second. Now let’s look at where we are, and where we want to be:
- Initially, we have a certain (known) angle, and angular velocity
- We want to end up at the angle indicated by the velocity change (yellow arrow) after a certain amount of time.
- At the time we get there, the angular velocity must be zero. This is necessary to prevent overshoot.
If you’re keeping count, these are four scalar constraints. We can therefore fit a four-parameter curve to these constraints. The easiest way to do this is to use a cubic polynomial. It might look like this:
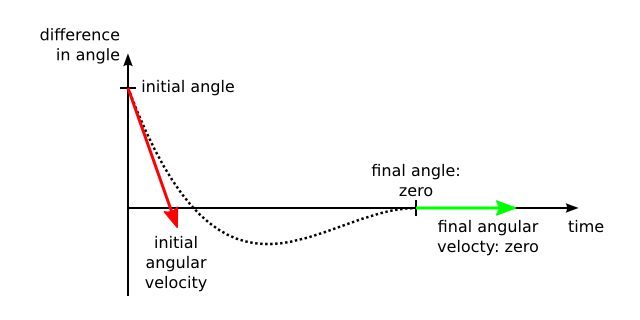
Notice that the example graph first overshoots the target. This can happen, if the angular velocity is so large that we cannot stabilize it on time. According to the laws of Newton, the angular velocity only changes if we push; this push incurs an angular acceleration. That acceleration exactly corresponds to the second derivative of the above graph, or, loosely said, the curvature. So if we compute the shape of the graph, then compute its second derivative, we know how hard to push. Problem solved!
Too bad that this is only half of the story. We don’t just want to point the cart in the right direction, we also need to fire the thrusters in a straight line afterwards. Preferably, we want to start doing a bit of both when we get close to the right direction. The current decision algorithm is based on ‘cost’ parameters: a wrong angle costs this much per degree, a wrong velocity costs this much per metre/second. Whichever cost ends up higher, we try to eliminate first. This works fairly well, but I’m not entirely happy yet (there’s that other 90% …).
To figure out what effect each thruster will have, some more math and physics were needed. Firing just one thruster causes the cart to spin, but also to move. Part of the force is ‘used’ for a linear velocity, part for an angular velocity. How big these parts are, depends on the location where the force is applied:
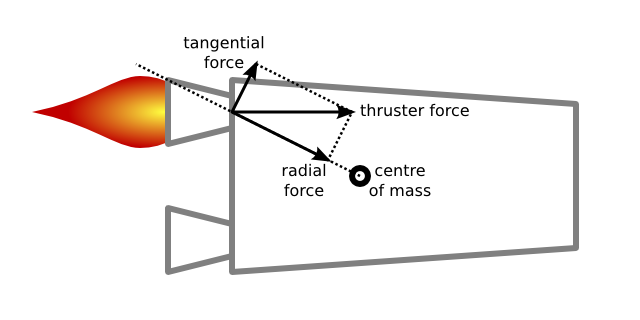
The force applied by a thruster is decomposed into two orthogonal components. The radial component, in the direction of the centre of mass, causes linear movement; the tangential component, perpendicular to that, causes the cart to spin. Armed with this knowledge, the Driver can now compute the amount of thrust needed to achieve the desired changes in linear and angular velocity. It’s remarkable that humans can control rocket-propelled shopping carts naturally, without any of the equations …
Finally, to improve realism and decrease CPU usage, I implemented some time intervals. The Driver will only look up his current situation once every 0.1 seconds, and only act upon this knowledge once every 0.1 seconds. I can change each of these intervals at will to alter the response time of the Driver. To prevent all AI drivers updating in the same frame, these ‘clocks’ are offset by a random time. As a bonus, sometimes the ‘acting’ will happen shortly after the ‘observing’, but sometimes it will take longer. This simulates the Driver having a good or a bad day, maybe depending on how well he slept or how much coffee he’s had. AI programming is so much fun …