Ballistics distance
Just a short post to share something I’ve been working on that mightily pleases the Kerbal Space Program player in me. In testing Orbital Express, it became clear that having three controls (compass direction, inclination, and launch speed) is too much for beginning players. So I decided to simplify the first two levels:
- Level 1: Only worry about compass direction; inclination and speed are automatic.
- Level 2: You now need to set speed as well; inclination is still automatic.
- Level 3: All controls are active.
However, now I had to figure out what “automatic” means. Of course the autopilot tries to get you as close to your target as possible. So I needed some way to convert the target distance back to the launch speed. Elevation can be kept fixed, because 45 degrees is pretty close to optimal.
The game computes rocket trajectories by just a simple “forward Euler” method, because I was too lazy to figure out the exact math for computing the orbit analytically. I had a look at that math again now, but it was still difficult, and I couldn’t figure out at a glance whether what I wanted was even possible analytically.
So back to a more braindead method: just launch at various speeds, see how far you get, and note the values in an array. When you need to compute a launch speed, do a linear interpolation between the two closest values in the array, and it should be pretty nearly optimal. This is what I’m implementing right now.
As a side effect, I also plotted the distance as a function of speed and inclination, courtesy of some hacky Java code, a CSV file and some Python, numpy and matplotlib:
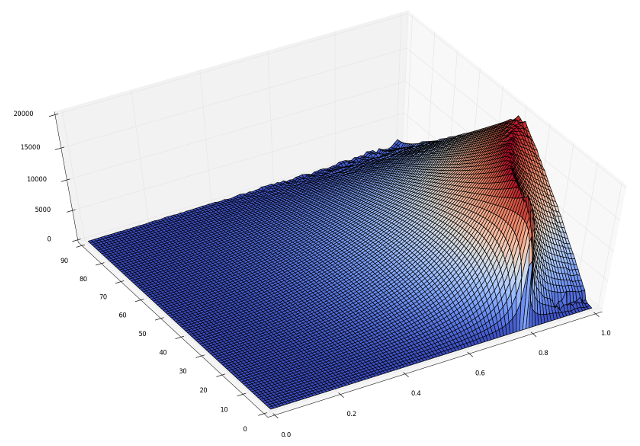
Launch speed is on the left-to-right axis, ranging from 0 to 90% of escape velocity. (Escaping Earth’s gravity leads to an infinite loop in the code, so I had to have some safety margin.) Inclination in degrees above the horizon is on the front-to-back axis. The height of the surface represents the distance travelled in kilometres.
The “ridge” here is interesting. That represents the distance to a point exactly opposite from you on the globe. The “valley” behind it represents circling back to almost where you came from, essentially shooting yourself in the behind.
It is also clear that the optimal launch inclination is not 45 degrees at all. The higher the launch speed, the flatter the trajectory needs to be in order to maximize distance (except beyond the ridge, where more distance travelled is less distance achieved). This makes sense because launching more horizontally will let you work more with the Earth’s gravity, instead of against it.
This doesn’t really matter for the first two levels (where all cities are close by), but it can make for an interesting challenge in later levels: the player could get a “frugality bonus” if they manage to hit the target with somewhere near the lowest possible launch speed. Something to think about.