Twistago AI, part 1: Easy
This is the first part of a three-part series in which I explain how the artificial intelligence works in my latest game, Twistago. The AI has three different levels: easy, normal and hard. This is also the order in which I developed them, each level building upon the lessons and code of the previous, so it’s only natural that I do this writeup in that order as well, starting with the Easy level.
Let’s begin with an overview of the game rules. I won’t explain every detail, but I’ll focus instead on the parts you need to understand the rest of this post.
Game rules
Twistago is played by 2 to 4 players on an unusually shaped board made up of squares, where each square can hold a playing piece as you might expect. For 4 players, this is the starting situation:

With 2 players, only red and green participate. If we add yellow to play with 3 players, the setup becomes asymmetric, but experience has shown that this doesn’t lead to significant imbalances.
The unusual thing about Twistago is the way pieces are moved. Notice the circles on the board above? Each move consists of turning one of these clockwise by a quarter turn (90 degrees). You can only move a circle that contains at least one of your own pieces, but every other piece in that circle moves as well:

The piece with the halo is called the commander, which can (but does not have to) move twice in a row.
The aim of the game is, roughly, to get your pieces to the mothership, the big same-coloured sphere at the other end of the board. I say “roughly” because there are other ways to win, and the actual winner is simply the player who gathered the most points, provided they also brought their commander home. Each piece brought home is worth 10 points. The game ends when a player can no longer make any move.
You may have noticed that the squares in the centre look unusual. This is the black hole (for lack of a better name, because it’s entirely unphysical, and dark blue to boot). Arranged around that are eight purple spheres called power cores. If you drop one of these into the black hole, it gets pulled home to your mothership for an additional 6 points. Another way to gain power cores is to land pieces (anyone’s pieces) into their mothership. If at that moment the black hole contains a power core, it becomes yours.
However, if a player piece is dropped into the black hole, it will remain there until it is liberated. While stuck, the piece is worth -10 points. You can liberate a piece by paying a power core, which subsequently goes into the black hole. Note that this gains you 10 points because the piece is no longer stuck, but costs 6 points because you lose the power core.
This mechanic is core to the game, because it gives rise to a high-risk, high-reward strategy. Dropping your own pieces into the black hole can be a massive shortcut that lets you get your pieces home quicker (and thus get more of them home before the game ends). This comes at the cost of a temporary setback in score (-10 points) and a permanent one (-6 points) for the power core payment. The latter can be recovered if you manage to land that piece quickly, so it’s crucial to time the rescue properly so your piece will be the first to land. Another risk is that other players drop more of your pieces into the black hole, and you won’t have enough power cores to rescue them all.
I think that’s enough of the ruleset to get started with. Now how do we make a computer play this game?
Testing and evaluating
Testing AIs can be rather tedious. You need to play lots of games against it to get a feel for how it behaves, and whether there are any situations in which it makes obviously bad moves. You should also vary your own strategy while doing this, to make sure there is no dominant strategy that will consistently beat the AI.
Although such manual testing remains important, for a first evaluation I wanted to have something more automated. So I built a framework that lets different AIs play a large number of games against each other, and tallies up the results:
Tournament finished after 913 ms
EasyStrategy: 56 wins (avg: 0 ms, max: 45 ms per move)
EasyStrategy: 44 wins (avg: 0 ms, max: 34 ms per move)
In this way, I could say: A beats B on 73 out of 100 games, so A is probably an improvement. I’m saying “probably” because for all I know, A exploits a weakness that B has, while having an even bigger weakness of its own that B doesn’t know about. So this approach is not perfect, but it can help to figure out whether you’re headed in the right direction, and helps to discover any blatant bugs like always moving in the wrong direction.
That was the original reason why I wrote this framework, but it turned out to have many more advantages. It doubled as a performance benchmark, which became important for the Hard AI where I needed every last bit of speed. Because the framework served up deterministically random starting situations, I could also use it to check that code changes didn’t affect the AI’s behaviour unless I meant them to. Finally, as an unexpected bonus, the framework served as a fuzz tester, outright crashing the program in some edge cases and finding bugs that would otherwise only have cropped up in production.
The drawback of such a framework is that it’s a black box: code goes in, number comes out. You have no idea what actually happened during these hundreds or thousands of games. So I also wrote some code to dump each game to a file, tagged in the filename with the name of the winning AI. These files could be played back in the game’s GUI, so I could manually dig into questions like “why did the Normal AI still lose these 5 games when it should be much better”?
As a properly trained software monkey, I also wrote some unit tests, but found that their use was limited. The trouble is that you don’t know the right answer, per se. Which is better in chess, to open with your king’s pawn or queen’s pawn? There are situations where the right move (or set of possibly right moves) is obvious, and those are the ones I gradually gathered up and added test for, but in most cases it’s hard to tell and thus hard to test.
Easy AI
As a first stick in the ground, I wrote an extremely simple AI that just picks a move at random (but as always, deterministically). This would serve as my benchmark that the Easy AI should consistently be able to beat.
How to improve on random movement? You might think: evaluate all possible moves, and pick the “best” one. No! That way, you end up focusing on the wrong thing. The thing that matters is not the move, but the eventual situation, or state. It does not matter how you ended up in that state! So we should evaluate the quality of the state after each possible move, and pick the move that maximizes that quality. The function that evaluates a state is technically called evaluation function but I’m calling it value function for short. As an added benefit, this somewhat decouples the AI from the movement rules: if the rules change to add a new kind of movement, the AI will just keep on working (although probably in a degraded way).
Since the aim of the game is to maximize your score, the obvious choice for a value function is the player’s score. However, this does not work. The score is not a nice, smooth function of game state: for most of the time it doesn’t change at all, and then it suddenly jumps. If we go by score, the AI would have no idea where to go unless it could get there in one move!
So we do need to start incorporating some of the game rules. The most basic thing that the AI should do is move its pieces towards the mothership. To make that happen, we need to construct the value function in such a way that states with pieces closer to the mothership receive a higher value than states with pieces farther away. So for each position on the board, we compute how many moves it takes from there for each player to reach their mothership (the small red and green numbers):
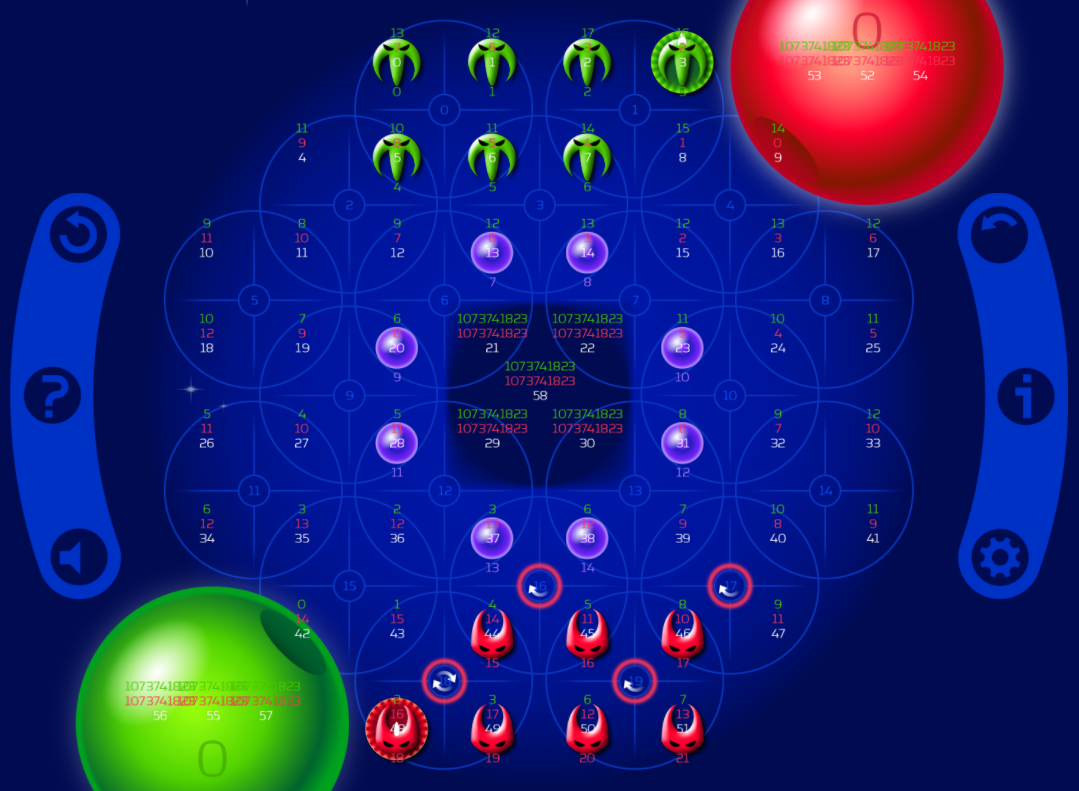
It’s really simple then: for each piece, take this distance, add them all up, and put a minus sign in front to make sure the value increases as the distance decreases. Bonus: moves that bring more than one piece forwards represent a bigger increase in value, so these will be preferred. This worked and consistently beat the random AI (which would just end up throwing itself into the black hole all the time).
To make sure that actually landing pieces is preferred over any old move, and especially to stimulate rescues and shed the -10 penalty, we also incorporate score into the equation. Now we’re adding two different sorts of quantities, distance and score, so we need to introduce some sort of weighing factor for each. Tweaking such factors was a large part of the work, especially as the number of terms grew. Look forward to the third part of this series on how I eventually managed to automate that!
Another game rule we need to account for is that the commander must be brought home in order to qualify for winning. This rule exists so you can’t keep your commander back forever harassing other players and preventing them from landing. The obvious way to make the AI aware of this rule is to award extra points for moving the commander forwards. However, then the AI race the commander to the finish right from the start of the game, which is an unnatural and bad strategy. Instead, the AI computes the difference between its commander’s distance and that of other players. If the AI notices that its commander is falling behind, it will catch up, but otherwise it’s free to use it for more local tactical advantage.
And how about taking other players into account? If the AI purely focuses on its own progress, it might end up accidentally giving points away. It might be nice to avoid this. In a two-player game, it doesn’t matter whether I gain 10 points, or I make you lose 10 points, so there it’s a simple matter of subtracting the opponent’s score from mine. In other words, instead of maximizing the AI’s own score, we maximize the amount of points by which it’s ahead of its opponent.
But how do you model this in a game with more than two players? Maybe it’s worse to accidentally give points to a player that’s in the lead? Then again, maybe they’re so far ahead that it doesn’t even matter anymore? Or maybe it’s worse to give points to a player that’s behind, because we want to keep them there? Then again, maybe they’re so far behind that it’s moot? Maybe it’s worst to give points to players whose score is close to mine, because that is most likely to matter for my eventual ranking? Heck, maybe I should give some points to the yellow player, so they might feel more kindly towards me when they have such a choice to make. These are hard questions, with a lot of active research behind them, so of course I did not manage to find good answers. I just computed the unweighted average of the scores of all opponents, and subtract that from the value function. This is just a generalization of the 2-player case.
So in the end, we have an AI that evaluates states based on relative score, piece distances and commanders’ relative locations, and picks the move that maximizes that value. The main thing it doesn’t do is try to look ahead further than that. By pursuing a local, small increase in value, it might miss out on a bigger opportunity one or two moves ahead. Because of this, it can easily be led into a trap, and it will never take a shortcut through the black hole. A perfect opponent for novice players, but a bore once they gain some experience. How can we do better? That will be the subject of part 2 of this series: the Normal AI!