Twistago AI, part 2: Normal
This is the second part of a three-part series in which I explain how the artificial intelligence works in my latest game, Twistago. In case you missed the first part, you can catch up on it here.
As you may recall, the Easy AI works by applying a value function to the end state resulting from each possible move, then picks the move that gives the highest possible value. The main problem with this is that the AI doesn’t look ahead: sometimes it should make a suboptimal move now, in order to get a higher gain in the future. This “higher gain” can either be a gain in the literal sense, or the avoidance of a loss (for instance, being sunk into the black hole by an opponent).
The minimax algorithm
The idea for making the AI look further into the future is straightforward. Instead of just evaluating the state after each of its possible own moves, it evaluates after each subsequent countermove by the opponent(s). And we can go even deeper: after the countermove, the AI can evaluate which moves are then available to itself, and so on. This gives rise to the notion of a game tree of a particular depth. For example, suppose there are two players, called “us” (the AI) and “them” (its opponent), and we’re going down to a depth of 2, the game tree could look as follows:
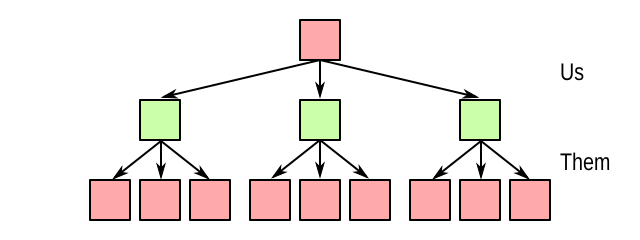
So we evaluate the state after one of our own moves followed by one of our opponent’s moves. Suppose the value function returns the following values:
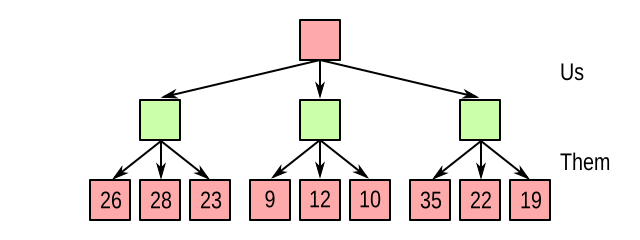
How does this tell us which move to make? Naively, you might think we take the branch containing the highest value, namely the rightmost one (35). However, right before that state, it was our opponent who made a move. Are they likely to help us get to that juicy 35? Not exactly. If we follow the rightmost path, the opponent will probably take the branch on the far right, resulting in a value of 19 for us.
From that, you can see we should assume that the opponent will do the worst possible thing for us. In other words, they will try to minimize our score. So if it’s the opponent’s turn, we take the minimum value of the outgoing branches, to end up with this:
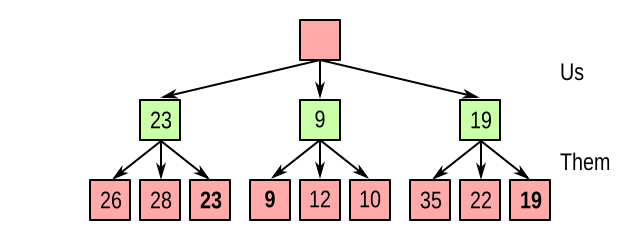
But to reach any of the states in the middle layer, we know it’s our move, so we get to pick which branch to take. And of course we take the maximum:
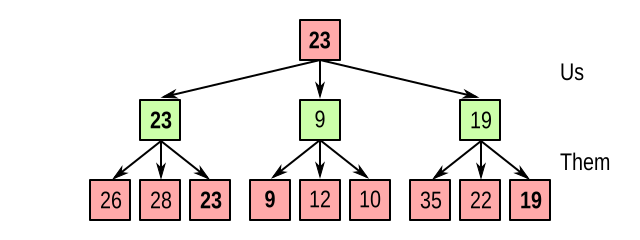
So the rule is: working from the bottom, if it’s the opponent’s turn, propagate the minimum value upwards, but if it’s our turn, propagate the maximum value upwards. This is the minimax algorithm, which stands for minimizing the maximum loss.
Performance
In the example above, I pretended that there were always 3 possible moves. This number is called the branching factor. In general, of course, it is not always the same, and might be much bigger. What is it like in Twistago in practice?
First, note that a player may take multiple actions during their turn. We consider the entire sequence of actions to be one “move”, so that after a move, we are certain that it’s the next player’s turn. In the worst case, a turn can consist of:
- A regular spin: 7 pieces, each in 2 cicles (14 options), plus a second move for the commander (4 options): 18 options in total.
- A choice of 6 pieces to beam home after sinking an opponent: 6 options.
- A possible rescue from the black hole to one of 8 positions around it: 8 options.
So in the worst case, we may have a branching factor of 18 × 6 × 8 = 864! Now this is still a relatively small number for a computer, but bear in mind that the game tree grows exponentially as it gets deeper: for a depth of 2, we are already looking at a worst case of 864² = 746k. On an average mobile device, we can evaluate about 10k positions per second, so even this rather shallow case would require over a minute of thinking time!
Fortunately, it’s not quite as bad as this. During the many AI-vs-AI matches, I measured the branching factor, and found that the average is around 13. However, cases of 100 or more do happen in practice, so we need to take these into account.
But even with a branching factor of 13, things get hairy rather quickly. Suppose we’re playing with 4 players, and we want to look ahead up to and including our own next turn, so we need a tree depth of 5. On average, such a tree would have 13⁵ = 371k leaves – still over half a minute of thinking time, so clearly unacceptable!
Alpha-beta pruning
Fortunately, techniques exist to reduce the number of states we have to evaluate. Consider again our example game tree, and suppose we’re running our minimax algorithm from left to right. We just evaluated our leftmost node:
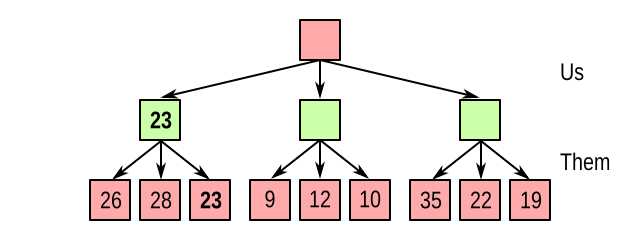
So whatever else happens, we are certain that we can achieve at least 23. We pocket this value, and call it alpha. Now we start evaluating the middle node, and immediately see that the opponent can make a countermove leading to a value of 9, which is less than 23. So there is no point in evaluating the other child nodes: we already know for certain that this node is a worse choice than the left one:
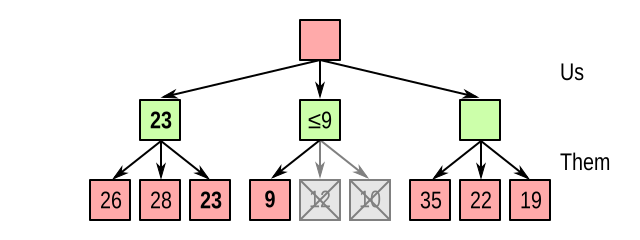
A similar thing happens in the rightmost node; although it looks promising at first when we see 35, the subsequent 22 also allows us to stop processing:
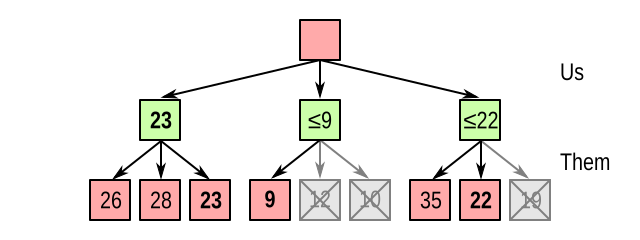
So in this case, we were able to eliminate 3 out of 9 nodes without even needing to evaluate them. Not bad! A similar thing can be done with the minimum value the opponent can achieve, called beta. And this is why this algorithm is called alpha-beta pruning.
The profit is even better if a large subtree is dangling beneath a node that is cut. Note that alpha-beta pruning is sensitive to ordering: if we manage to look at the “best” nodes first, alpha-beta pruning will let us evaluate a tree twice as deep (and thus with the number of nodes squared) compared to naive minimax. If we get the ordering exactly wrong, it degrades to regular minimax, so we haven’t lost anything. But even if we get the ordering approximately right, the gains are substantial.
So how do we order the “most promising” nodes first? Simple: run each through the evaluation function, and order the nodes by decreasing value. If a move increases our value now, it’s more likely – though by no means guaranteed – to be a good move in the long run.
Tearing off more branches
Even with alpha-beta pruning in place, evaluating the game tree to a reasonable depth would sometimes still take too long. This was caused by nodes with the near-worst-case 100+ branching factor. If one of these happens at the root, the explosion of subtrees was more than a poor mobile device could handle.
In these situations, I applied a really blunt instrument: evaluate only the first n “most promising” moves, then stop. In theory, this may result in some brilliant tactics being overlooked, but in practice, most of the “less promising” moves contain a really bad rescue from the black hole and are not worth bothering with.
Similarly, I also applied some pruning heuristics to eliminate moves that I knew, from the game rules, to be always a bad idea, such as rescueing a piece into a place where the opponent can immediately drop it back into the black hole again. This made the AI always complete its thinking process within a second or two.
Multiple opponents
In the first part, I already talked about the difficulties of modelling a game with more than two players. When given a choice, which player should we help or hinder? With minimax, another complication gets added to the mix: how should we apply the minimax algorithm if there’s more than one opponent? Remember that we always try to maximize our value, and “the opponent” always tries to minimize it. Is this still true when there’s more than one opponent?
The simplest way is to answer this with “yes”. There are multiple opponents, each gets their own turn as a level in the game tree, and each will find the minimum of its child nodes. The underlying assumption here is that all opponents are out to minimize my value, and will even collaborate to do so; in other words, they’re “ganging up” on me. This assumption may lead to very defensive, paranoid play by the AI.
Another idea I played around with is to “merge” all opponents into one, who gets to make a single move before it’s my turn again. This is another way to reduce the multiplayer game back to a 2-player game. It is representative only in cases where sequences of multiple moves (deliberately or not) would affect our state differently than each move individually. For instance, if one player moves our piece to the edge of the black hole, then the next player throws us in, the AI would not be able to detect this possibility. In practice, that turned out to be a big weakness, so I had to abandon this approach.
More realistically, we could continue to model multiple opponents. But instead of all minimizing our value, they will try to maximize a value function of their own. This is the idea behind the max^n algorithm (Luckhardt and Irani, 1986). However, it makes matters much more complicated. Now we need to figure out how they compute their value. Do they use the same value function we do, applied to their own pieces? Or do they employ a different strategy? Even if we pretend that everyone uses the same value function, there is another problem: because each node gets evaluated not by 1, but by 4 different functions, alpha-beta pruning no longer works, and pruning strategies in max^n are severely limited (Sturtevant, 2000).
Fortunately for me, the “paranoid” approach has been shown (Sturtevant, 2002) to be much better than max^n in Chinese Checkers, a game which is somewhat similar to Twistago:
These results show that the paranoid algorithm is winning in Chinese Checkers both because it can search deeper, and because its analysis produces better play. We would expect similar results for similar board games.
I tinkered around with max^n at some point, but based on this result, I decided not to pursue it further, and stuck with the paranoid algorithm. With some more tweaks to the value function, I managed to get the Normal AI to a decent enough state that it was able to beat me about half the time. Unlike the Easy AI, the Normal one would occasionally take a shortcut through the black hole, because it would see that the reduction in value was only temporary and would be compensated by a larger increase a few moves from now.
So why didn’t it beat me all the time? What improvements could still be made? One weakness was that the AI had no notion of how close to the end the game was, so it wouldn’t adapt its strategy accordingly. For example, at the start of the game, it’s a good idea to gather power cores while you can, but later on, getting your aliens home quickly becomes more relevant. Another weakness was that, because of all the worst-case scenarios I had to account for, the average case would require less than a second of processing time. It’s okay to make the human player wait for maybe 3 to 5 seconds, if only we knew how to make use of that extra time. These potential improvements, and more, will be the subject of the third and final part of this series: the Hard AI!