Around The World, Part 4: Basic wind
Now that we have a finalized height map of our generated world, it’s time to put something on the surface. But to know what to put there – forest, desert, grassland, ice – we have to know something about the local conditions. And to know those, we have to know about wind patterns.
Another reason why wind is important, is that this will be a sailing game. My goal for this episode is to generate a static pattern of prevailing winds. That is, wind doesn’t vary over time; we’ll add this later. At each point on the planet, we’ll have a velocity vector representing the x (eastwards) and y (northwards) components of the wind, but you can think of it as a compass direction and wind speed if you prefer.
Atmospheric circulation, like plate tectonics, is another deep rabbit hole full of PhDs. I’m not going for full realism here, not only because it’s too difficult to program, but also because it’s too slow to calculate. So let’s see how far we can get with relatively simple methods. To cause offense to at least three subject areas at once, I’ll be playing fast and loose with meteorological, physical and mathematical concepts here – don’t say I didn’t warn you.
Straight and simple
Wind is driven by areas of low and high pressure. Near the equator, the surface of the Earth is heated the most by the sun. This causes the air to heat, expand and rise, lowering the pressure near the surface and sucking in air from higher latitudes. Higher up, the inverse happens, giving rise to the Hadley cells:
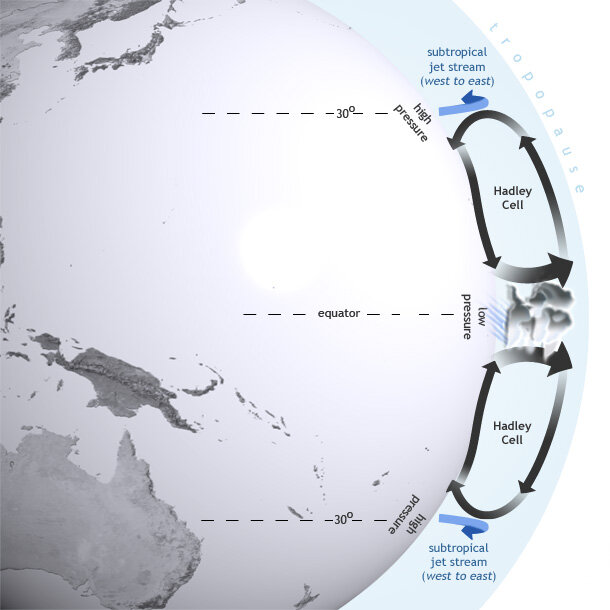
As you can see, between 0° and 30° latitude there is a general tendency for wind to blow towards the equator. Between 30° and 60°, the wind blows away from the equator due to the Ferrel cells, and between 60° and the poles, due to the polar cells, it blows towards the equator again.
This is of course a massive simplification, but we can code it up easily to make sure everything is working:

Looks like it’s working indeed! Instead of hardcoding this latitude dependence, I decided to make it data-driven, so it’s all based on easily editable curves like these:
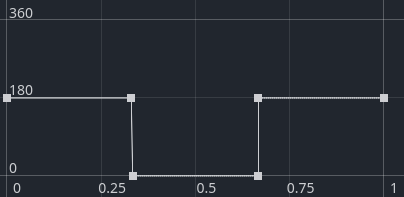
The horizontal axis goes from the equator to the poles, and the vertical axis is the degrees north or south that the wind is blowing.
Coriolis
The next effect to account for is the Coriolis force. Due to the rotation of the Earth, any object moving along its surface experiences a force that pushes it off the straight path. You don’t normally notice this because the force is so weak, but on large amounts of moving air, it has a significant influence. Here’s a simplified image that shows how the Coriolis effect causes the winds to veer away from their straight vertical path:
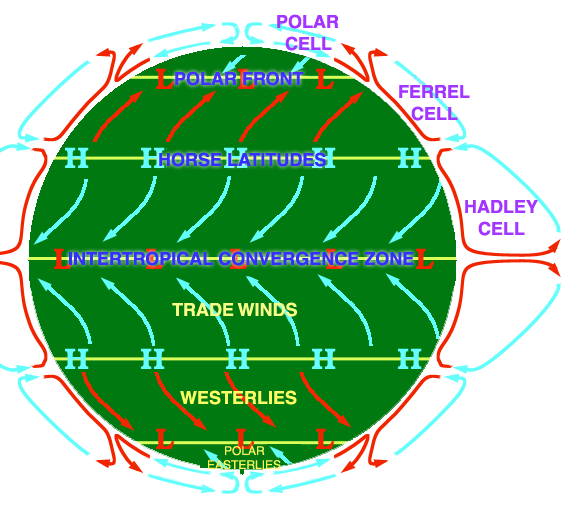
Image by DWindrim from Wikimedia Commons, CC-BY-SA 3.0
That’s easy now! We just edit the curve to make the bearing gradually change with latitude:
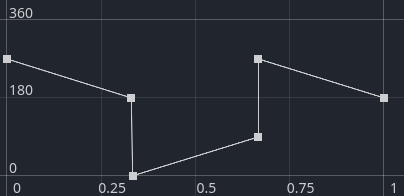
And ta-da:

Terrain effects
So far, I’ve been pretending that the planet is a perfectly smooth sphere. But we know that the flow of air is slowed down over land, due to friction. We can easily mimic that by halving the speed of wind on land:

It may be hard to see, but the stream lines over land did become shorter, indicating a lower speed.
Now we get to the difficult bit. Not just the speed of wind is affected by the terrain, but also its direction. Wind blowing into a coast or mountain range tends to get deflected sideways (besides getting slowed down). In addition to that, and unrelated to friction, wind going uphill loses speed because it has to battle against gravity. Wind going downhill gains speed because it has gravity working for it.
Thinking about this for a while, I realized it all comes down to the gradient of the terrain, i.e. the arrow that points in the steepest uphill direction. It’s always the case that the air experiences a force in the opposite direction of the gradient, i.e. in the steepest downhill direction. The force is proportional to the steepness. This force doesn’t just account for the slowing down and speeding up, but also for turning the wind sideways (unless it’s exactly in line with the gradient).
So let’s add that and see where it leads. I’ve zoomed in a bit on an interesting part of terrain:
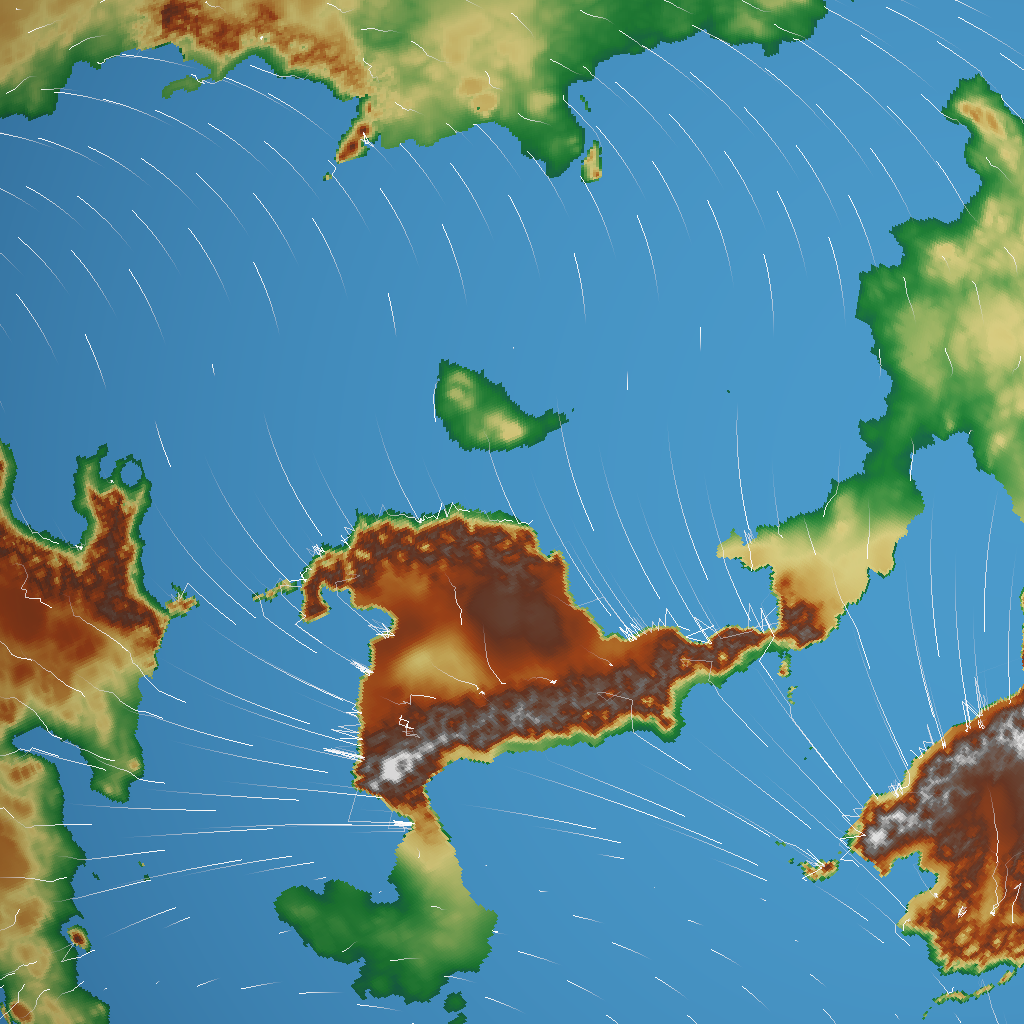
Whoops! That doesn’t look like wind – it looks more like a hailstorm is bouncing off the coast. What happens here is that the wind from the sea and the wind from the land meet with a very sharp boundary in between, causing the streamline to bounce back and forth.
The problem isn’t that the effect is too strong, the problem is that it’s too local. So I tried blurring the wind map; the wind vector at each point takes on some of the strength and direction of its neighbours:
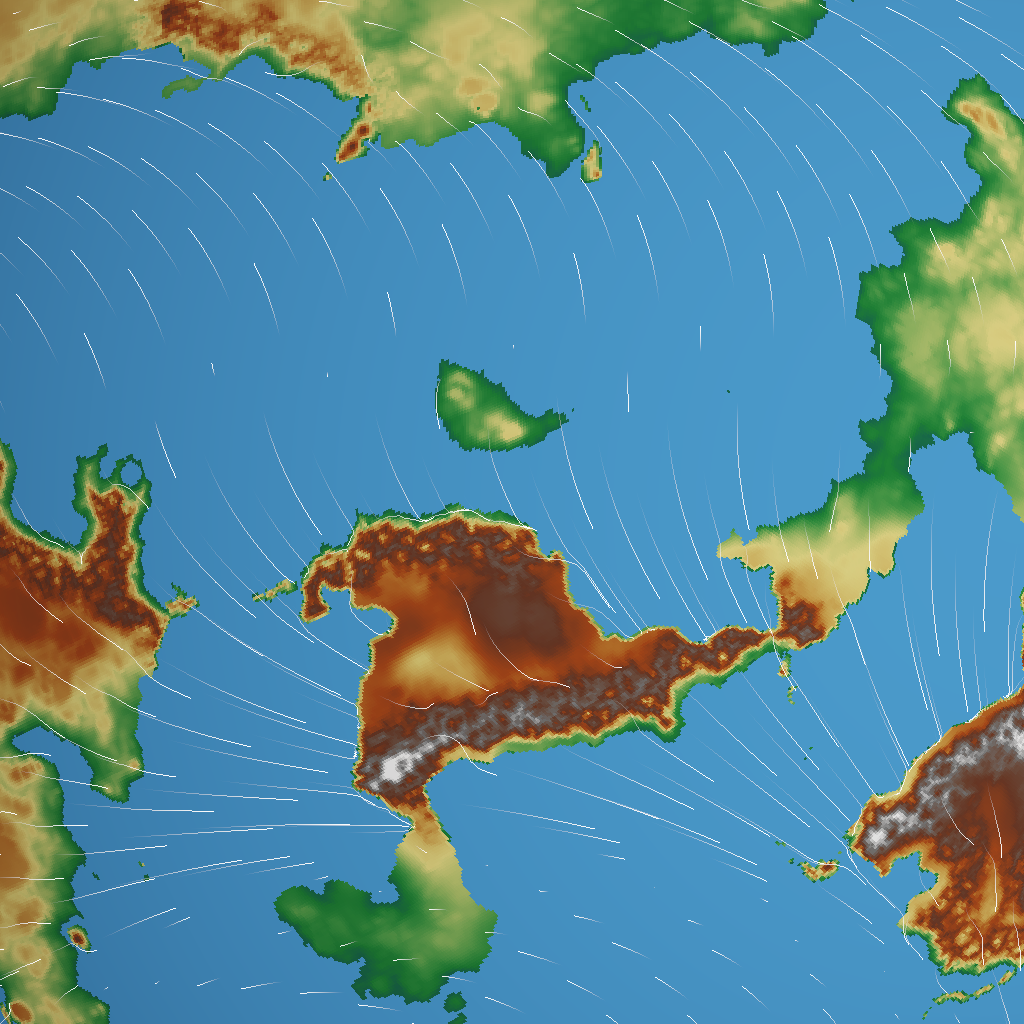
Better! You can see how the wind is now deflected by the coastlines and mountain ranges.